Understanding Mathematical Reasoning of LLMs

What does it mean for LLMs to do mathematics?

Introduction

As an AI researcher with a background in pure mathematics and physics, I am interested in the interplay between formal logic and machine learning. Recent advances in large language models (LLMs) and their ability to potentially solve complex mathematical problems has opened up interesting research directions. This ‘mathematical reasoning’ - requiring rigorous logic, precise symbolic manipulation, and structured problem-solving - remains a subject of intense personal fascination. Unlike natural language tasks, where ambiguity and flexibility are often strengths, mathematical reasoning demands accuracy, consistency, and the ability to navigate abstract concepts, posing unique challenges for LLMs trained for next token prediction.

While it is not hard to imagine these models solve simple arithmetic or mimic problem-solving steps from training data. However, tasks involving deeper reasoning such as constructing proofs, parsing complex word problems, or generalizing beyond seen examples do pose a challenge. Whether LLMs truly reason mathematically or merely parrot patterns from their training data is a quite an interesting question. Nevertheless, such an intelligent system could have strong implications for education (e.g., AI tutors), scientific research (automated hypothesis testing), and safety-critical applications (engineering or finance), where reliability is paramount.

In this work, I study the mathematical reasoning of small LLMs trying to build an understanding of the mathematical prowess of LLMs.

Mathematical Reasoning: Why does it matter?

Mathematical reasoning is at the heart of intelligence. Unlike simple pattern matching or memorization, reasoning involves structured problem-solving, logical deduction, and generalization. It has been seen that doing well on mathematical tasks has enhanced model performance in other domains as well. In an ideal scenario, an LLM that reasons mathematically would exhibit:

• The ability to break problems into intermediate steps.

• Logical consistency in its derivations.

• Adaptability to novel problems that are not explicitly present in its training data.

What It Means to Have Reasoning

For an LLM to be said to “reason,” it must exhibit behaviours such as:

• Understanding context: Interpreting word problems with variables, constraints, and dependencies.

• Step-by-step logic: Breaking problems into intermediate steps (e.g., “Find x first, then compute y”) and following logical sequences rather than relying on direct retrieval.

• Chain-of-Thought (CoT) Consistency: Producing coherent, valid step-by-step solutions that align with human mathematical reasoning.

• Error Correction: Identifying and fixing mistakes in intermediate steps.

• Generalization: Solving problems beyond training distribution by applying learned mathematical principles.

True reasoning requires more than pattern matching; it demands structured, causal thinking akin to human problem-solving.

How is mathematical reasoning cultivated?

LLMs like GPT-4 have been trained on vast corpora, which likely include mathematical texts like textbooks, papers, and online resources during pre-training gives them a foundational grasp of notation and basic concepts. This foundation enables basic arithmetic, algebraic manipulation, and familiarity with concepts like equations or geometry. However, this generaL pre-training alone is insufficient for complex reasoning, as mathematical rigor demands precision beyond statistical pattern-matching. Models may recognize common problem templates (e.g., quadratic equations) but fail at novel or multi-step challenges.

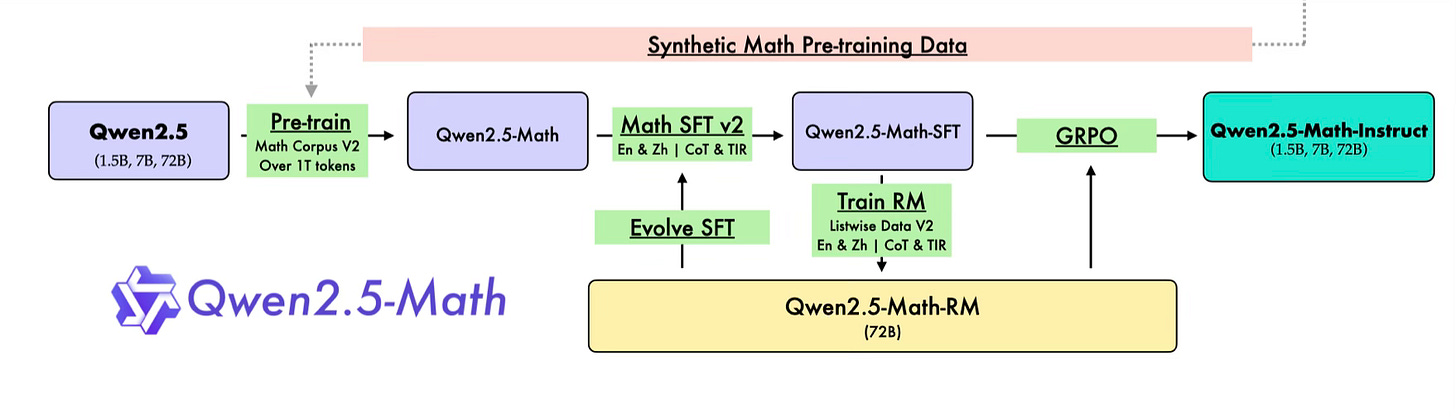
Specialized Pre-training: The Qwen team pre-trained their Math series of models on a meticulously designed mathematics-specific corpus containing large-scale high-quality mathematical web texts, books, codes, exam questions, and synthetic data. This helps in building a stronger foundation model for math. However, it is not capable to answer or solve math problems. To bridge this gap, models are fine-tuned on curated datasets of mathematical problems and solutions.

Chain-of-Thought - This involves supervised fine-tuning LLMs directly on curated or synthetic CoT data containing math problems and their detailed solutions. Human generated data, either pre-existing or by employed subject-matter experts, can be curated for SFT. This procedure is expected to train models to internalize step-by-step reasoning patterns by embedding them into the model’s parameters during fine-tuning.

Tool-Integrated Reasoning - This refers to the ability of LLMs to leverage external tools - such as search engines, calculators, code interpreters - to enhance their reasoning, problem-solving, and decision-making capabilities. Instead of relying solely on their parametric knowledge, LLMs can invoke these tools dynamically to perform tasks that require real-time information retrieval, numerical computation, or specialized domain expertise. In Qwen2.5-Math models, DeepSeekMath etc. they use python interpreter to improve the performance of their models.

Reinforcement Learning via Verifiable Rewards - Recently, the RL method Group Relative Policy Optimization (GRPO) has grained a lot of traction due to the success of DeepSeek-R1. This has been adapted in some studies (wilcbb, unsloth) to show that reasoning can emerge as a learned behavior through pure reinforcement learning (RL) on problem-answer data without requiring any CoT.

In practice, the whole setup for developing a state-of-the-art math model can be lot more complicated, for example, the Qwen2.5Math model pipeline looks like:

Current Work

This article examines the current state of mathematical reasoning in LLMs. This work stems from a desire to bridge the gap between published benchmarks - tables of accuracy percentages and scores - and a concrete (personal) understanding of what these metrics mean and signify about LLMs’ mathematical reasoning capabilities. This is the first report of the project of me trying to build a better understanding of LLM mathematical reasoning. The goal of current work is 3-fold:

1. Decode the results reported in scientific reports.

2. High-level investigation the mathematical reasoning of small LLMs.

3. What it means for reasoning.

In the future work, I will dig deeper to understand the mechanisms driving the performance of LLMs and to try to use the learnings to enhance the mathematical reasoning of the models.

Data

There are many benchmark datasets for math reasoning being used in scientific reporting like GSM8K, MATH etc. The data I used here is the AIME benchmark which is a dataset derived from the 2024 American Invitational Mathematics Examination (AIME), a prestigious high school mathematics competition in the United States. This benchmark is designed to evaluate the mathematical reasoning capabilities of large language models (LLMs) by presenting them with complex, multi-step problems that require advanced problem-solving skills.

Dataset Composition:

• Source: Contains 90 problems from AIME 22, AIME 23, and AIME 24, and have been extracted directly from the AOPS wiki page by the Project Numina.

• Content: The problems cover various mathematical domains, including geometry, algebra, and number theory.

• Format: Each entry includes a problem statement, a detailed solution, and the final numerical answer.

  • Problem: The original problem statement from the website

  • Solution: One of the solutions proposed in the AOPS forum in LaTeX format.

  • Answer: Actual numeric answer.

An example problem -

Quadratic polynomials $P(x)$ and $Q(x)$ have leading coefficients $2$ and $-2,$ respectively
The graphs of both polynomials pass through the two points $(16,54)$ and $(20,53).$ Find $P(0) + Q(0).$

Now this problem requires multiple steps with consistency to solve. One of the provided solutions is:

Let $R(x)=P(x)+Q(x).$ Since the $x^2$-terms of $P(x)$ and $Q(x)$ cancel, we conclude that $R(x)$ is a linear polynomial.
Note that
\begin{alignat*}{8} R(16) &= P(16)+Q(16) &&= 54+54 &&= 108, \\ R(20) &= P(20)+Q(20) &&= 53+53 &&= 106, \end{alignat*}
so the slope of $R(x)$ is $\frac{106-108}{20-16}=-\frac12.$
It follows that the equation of $R(x)$ is \[R(x)=-\frac12x+c\] for some constant $c,$ and we wish to find $R(0)=c.$
We substitute $x=20$ into this equation to get $106=-\frac12\cdot20+c,$ from which $c=\boxed{116}.$ 

Understanding Reported Benchmarks

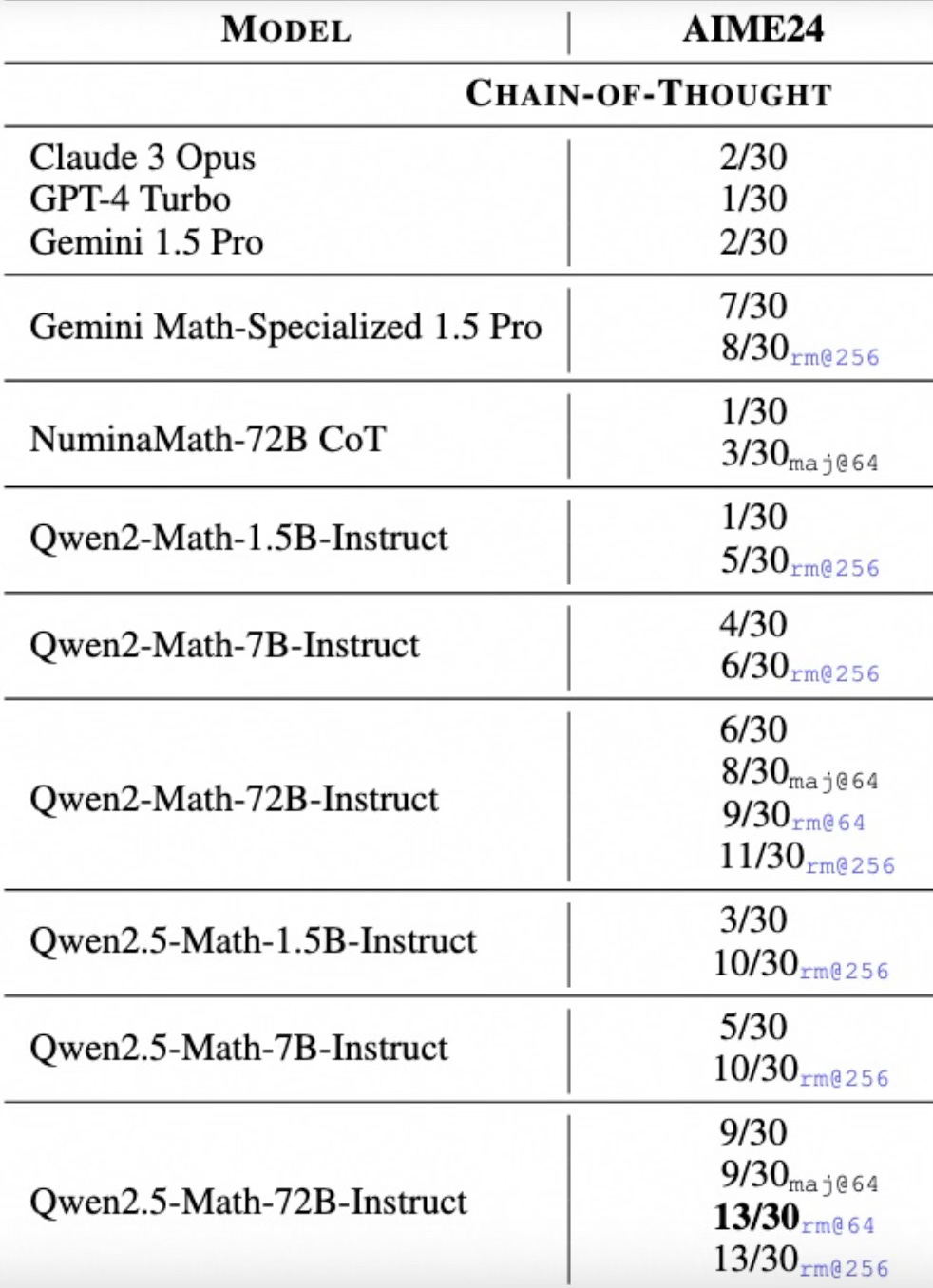
Let’s look at this table from Qwen2.5-Math report:

There are 30 problems in the AIME 2024 on which these results are reported. The results are produced in zero-shot setup i.e. no examples are provided for in-context learning. We can the best proposed model can only solve 13 out of 30 problems in the best case scenario. Let’s unpack this:

• Greedy Decoding: The model generates an answer by always selecting the most likely next token at each step without sampling. These are the numbers without a subscript e.g. 9/30 in the last row.

  • This typically results in deterministic outputs but may not explore diverse solutions.

• Maj@8 (Majority at 8): The model samples 8 different responses to a given problem. The final answer is chosen as the most frequent (majority vote) solution among those 8 samples.

  • This is useful for improving robustness, as the most common response among multiple runs is likely to be correct.

• RM@8 (Risk Minimization at 8): The model generates 8 different responses and then selects the one that minimizes risk, often determined by a ranking model or heuristic.

  • A ranking model (e.g., trained on correctness signals) could be used to choose the most promising response.

Why These Metrics?

• Greedy decoding is a baseline that shows how well the model performs deterministically.

• Maj@8 helps account for variance in generation and improves reliability by aggregating responses.

• RM@8 attempts to intelligently select the best response, potentially outperforming majority voting.

Evaluating a Model for Mathematical Reasoning

Given a model M, we would want to evaluate its performance and compare it with other models as shown in the table above. A model trying to solve a math problem would produce a blob of text which could contain the reasoning traces, steps of calculation, and the answer. Properly extracting the answer predicted by the model can be tricky, especially if we intend to compare the predicted answer with a ground truth, e.g., $2, USD 2, 2 USD, 1.9998$, 2 can all be correct answers. So, the first step in evaluation is to extract the answer from the response blob and compare it with the ground truth. Of course, for the Maj@k or RM@k setup, you would want to generate multiple responses for a given problem and choose the answer accordingly. As you can imagine, this can be quite arduous to clean the generated response to extract the answer. This is what math-evaluation-harness and Qwen2.5-Math-evaluation have done. I adapted the Qwen evaluation for this work.

Notably, the evaluation methods discussed thus far focus solely on final answers rather than the problem-solving process. In contrast, traditional math assessments typically require students to be graded on both their reasoning steps and their solutions. If we could disregard the methodology and evaluate only end results, grading papers would be a breeze (I know from personal experience, how dreaded is paper grading among teachers). In fact, we explicitly asked students to ‘show your work’ in papers. You can argue that the steps themselves - not just the final conclusion - serve as the truest reflection of mathematical understanding and reasoning.

Further, there is a larger question of how to evaluate the goodness of a model for mathematics. This can spur into the discussion on the choice (and possible lack) of benchmark datasets considering the possibility that any data that exists on the internet can potentially find its way into the model’s training data. This is an active discourse and new benchmarks like Frontier Maths etc. are being proposed.

Experiments:

I like to start in the realm of small models for prototyping and to build an understanding. In this work, I take a Qwen2.5-Math-1.5B-Instruct, the smallest model from Qwen2.5-Math family which are trained specifically for mathematical proficiency. As noted in the above table, this model can solve 3 out of 30 test problems in the AIME data. I was able to reproduce this result using the recipe from Qwen2.5-Math-evaluation. I am more interested in the problems the model was not able to solve, particularly the failure points and the lack of ‘reasoning’.

Two out of the three problems that the model solved are not too wordy and have the equations spelled out in the problem statement. The third one is a probability problem with simple numbers. You can argue these problems are ‘simpler’ or ‘easier’ in some sense. I am desperately looking for patterns here, it could all be random!

Let’s consider a relatively simple problem that the model failed to solve:

Every morning Aya goes for a $9$-kilometer-long walk and stops at a coffee shop afterwards. When she walks at a constant speed of $s$ kilometers per hour, the walk takes her 4 hours, including $t$ minutes spent in the coffee shop. When she walks $s+2$ kilometers per hour, the walk takes her 2 hours and 24 minutes, including $t$ minutes spent in the coffee shop. Suppose Aya walks at $s+\frac{1}{2}$ kilometers per hour. Find the number of minutes the walk takes her, including the $t$ minutes spent in the coffee shop.

Upon inspecting the generated solution, the first error is the model makes a wrong assertion that the time spent walking is same in both the cases. As a result, the equations it set to describe two situations are wrong. Translating a word problem into correct equations is an important dimension of mathematical reasoning. And so is utilising a hint.

Hints

To help the model, I add a hint to the prompt.

Hint: The time spent at the coffee shop is same in all the cases whereas the time spent walking is variable. Use this information to set up the equation.

Now, the model is able to use this information and set the correct equations. In fact, it correctly performs the computation and proposed the answer as 3 \text{ hours and } 24 \text{ minutes}. Only problem is that, in the end, it hastily returns the final answer as \boxed{324} by concatenating 3 hours and 24 mins. This way the model went from making a strategic error to an arithmetic error. This shows the model does have some mathematical

Obviously, hints presented in this form won’t always work. Curation of the most useful hint could be harder than solving the problem. In the following problem:

Each vertex of a regular octagon is independently colored either red or blue with equal probability. The probability that the octagon can then be rotated so that all of the blue vertices end up at positions where there were originally red vertices is $\\tfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. What is $m+n$?

The model made the wrong deduction that

This means that the number of blue vertices must be the same as the number of red vertices

which results in it missing the correct line of thought. I tried a few hints which didn’t work, it continued to make the same mistake. What seemed to at least steer the model in the right direction is adding a line from one of the solution to the ‘assistant’ content in the prompt messages. The model still made lot of mistakes further down.

The idea of providing hints to the model can be useful and can provide a test of their mathematical reasoning. There is also a larger topic of steering models in desirable directions. Formalising the idea of hints and devising a mechanism to automatically craft hints would be quite useful. The hints I experimented with were devised retrospectively after looking at the model response.

Grading a Solution

Different aspects of problem-solving like problem understanding, logical consistency, concept recall etc. provide a comprehensive assessment of mathematical reasoning. Consider the situation above where the model was able to arrive at the correct answer 3 hours and 24 mins, but translated that as 324 minutes. I can argue that the model does exhibit mathematical reasoning while solving this problem, albeit not perfect. I found multiple cases where the model correctly understood the problem and made an arithmetic error or wrote the equations incorrectly.

Look at the example:

Alice and Bob play the following game. A stack of $n$ tokens lies before them. The players take turns with Alice going first. On each turn, the player removes either $1$ token or $4$ tokens from the stack. Whoever removes the last token wins. Find the number of positive integers $n$ less than or equal to $2024$ for which there exists a strategy for Bob that guarantees that Bob will win the game regardless of Alice's play.

The model correctly identifies that the winning strategies occur when n ~ 5 mod 2, and computes the number of cases, but misses that the scenario n ~ 5 mod 0 is also a legit possibility. So the predicted answer is half (ish) of what is needed. The model did a good job understanding the word problem, comes up a good strategy, identifies one of the two cases and does correct calculation for the part.

Another example that I expected the model to solve given what it had solved:

Among the 900 residents of Aimeville, there are 195 who own a diamond ring, 367 who own a set of golf clubs, and 562 who own a garden spade. In addition, each of the 900 residents owns a bag of candy hearts. There are 437 residents who own exactly two of these things, and 234 residents who own exactly three of these things. Find the number of residents of Aimeville who own all four of these things.

The model makes a mistake in the equation which leads it to miss the answer.

Not all mistakes are equally harmful and they are not equally representative of mathematical reasoning. To dig a bit deeper into the mathematical prowess of LLMs, I prompted o1 reasoning model to ‘grade’ a solution to a problem based on the following dimensions, each with score between 0 and 4:

• Problem Understanding

• Setup and Strategy

• Mathematical Execution

• Correctness

The response of o1 is as follows:

{
  "problem_understanding": "<reasoning>The student demonstrates a clear understanding of the problem by correctly identifying that they need to find all positive integers \( n \leq 2024 \) for which Bob has a guaranteed winning strategy, regardless of Alice's moves. They appropriately use the concept of winning and losing positions in impartial games and apply it to analyze the game's outcomes.</reasoning><score>4</score>",
  "setup_and_strategy": "<reasoning>The student begins by identifying base cases and attempts to establish a pattern for winning and losing positions based on \( n \mod 5 \). They conclude that positions where \( n \equiv 2 \mod{5} \) are losing positions for Alice. However, they overlook that positions where \( n \equiv 0 \mod{5} \) are also losing positions for Alice, where Bob can employ a complementary strategy. This omission leads to an incomplete strategy.</reasoning><score>2</score>",
  "mathematical_execution": "<reasoning>The student correctly calculates the number of integers less than or equal to 2024 that are congruent to 2 modulo 5, finding 405 such numbers. However, by not accounting for the \( n \equiv 0 \mod{5} \) cases, which also represent losing positions for Alice, the mathematical execution is incomplete. This oversight results in an incorrect total count.</reasoning><score>2</score>",
  "correctness": "<reasoning>The student arrives at an answer of 405, accounting only for the cases where \( n \equiv 2 \mod{5} \). The correct answer is 809, which includes both \( n \equiv 2 \mod{5} \) and \( n \equiv 0 \mod{5} \) cases. By omitting half of the required cases, the final answer is significantly incorrect.</reasoning><score>1</score>"
}

I studied some of the responses to build a correlation with my (super biased) personal grading rubric. Here are the results for Qwen2.5-Math-1.5B model for performance on AIME 2024:

This is deeply flawed -

• Even o1 doesn’t have 100% accuracy on AIME. However, the assumption is that critique is ‘easier’ (?) than solving. A further enhancement can be using multiple models like o1 and DeepSeek.

• No prompt tuning was done, it would be useful to add tune the prompt to get the desired responses. Also providing a detailed rubric could help.

• The dimensions considered are far from exhaustive when it comes to mathematical reasoning. Adding other dimensions e.g. reflection, identifying errors etc. can further strengthen the grading mechanism.

Check out the math-reasoning repository for the notebook containing the codes I used here.

Discussion:

• Hints can help, though it is hard to think of the hint a priori. A well-formalised notion of hint can potentially improve reasoning in smaller models, and also serve as a dimension for evaluating the mathematical reasoning of models.

• A comprehensive evaluation of mathematical reasoning beyond the final answer matching would go a long way towards evaluating and improving the mathematical reasoning of LLMs. Here I create simple rubric for evaluation, which is obviously far from useable, but is meant to highlight the argument.

Conclusion

In this work, I investigated the mathematical reasoning LLMs. I explored the performance of a small model Qwen2.5-Math-1.5B on AIME dataset to build an intuition. The model does show some mathematical prowess, particularly in understanding word problems and shows logical consistency. They are obviously prone to mistakes which I attempted to understand better. This work highlights the need for more comprehensive evaluation when it comes to mathematical reasoning.

This is a starting point of my personal project of investigating the mathematical reasoning of LLMs. Please follow along for more such explorations.

If you find this work useful, I would appreciate if you cite it as:

@misc{verma2025math-reason,   
  title={Understanding Mathematical Reasoning of LLMs},      
  author={Janu Verma},   
  year={2025},   
  url={\url{https://januverma.substack.com/p/understanding-mathematical-reasoning}},   
  note={Incomplete Distillation} 
}