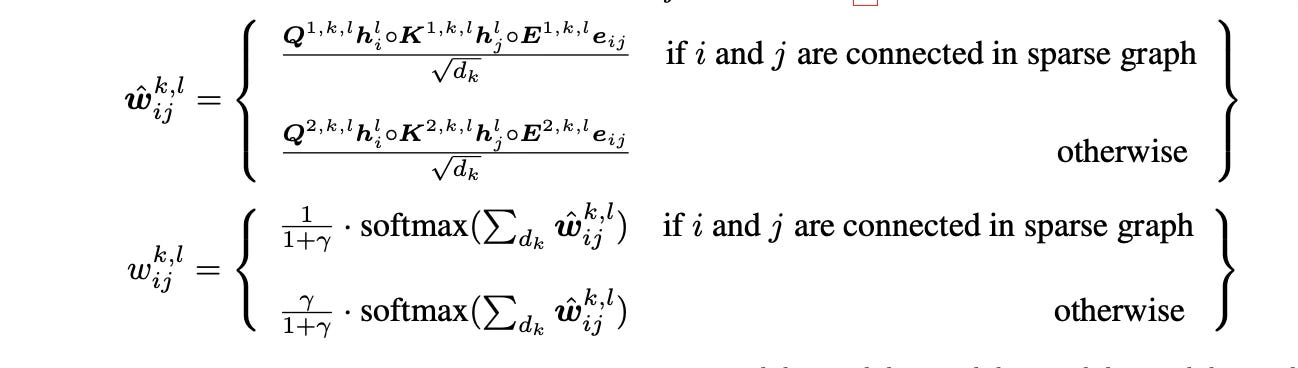Graph Transformers
From Message Passing to Global Attention
Introduction
Deep learning’s most spectacular successes share the same secret ingredient: an architecture that respects the geometric structure of the data. CNNs thrive because images are grids; LSTMs succeeded at language because sentences can be treated as sequences with long‑range dependencies. Real‐world systems such as molecules, power grids, social networks and knowledge graphs live on graphs which are irregular spaces where neither grids nor sequences offer much guidance.
Graph Neural Networks (GNNs) were the first general‑purpose attempt to learn on such domains. They delivered impressive results, but as datasets and ambitions grew, the field ran into fundamental bottlenecks. At their core, many GNNs operate on a principle called message passing.
The Message-Passing Paradigm
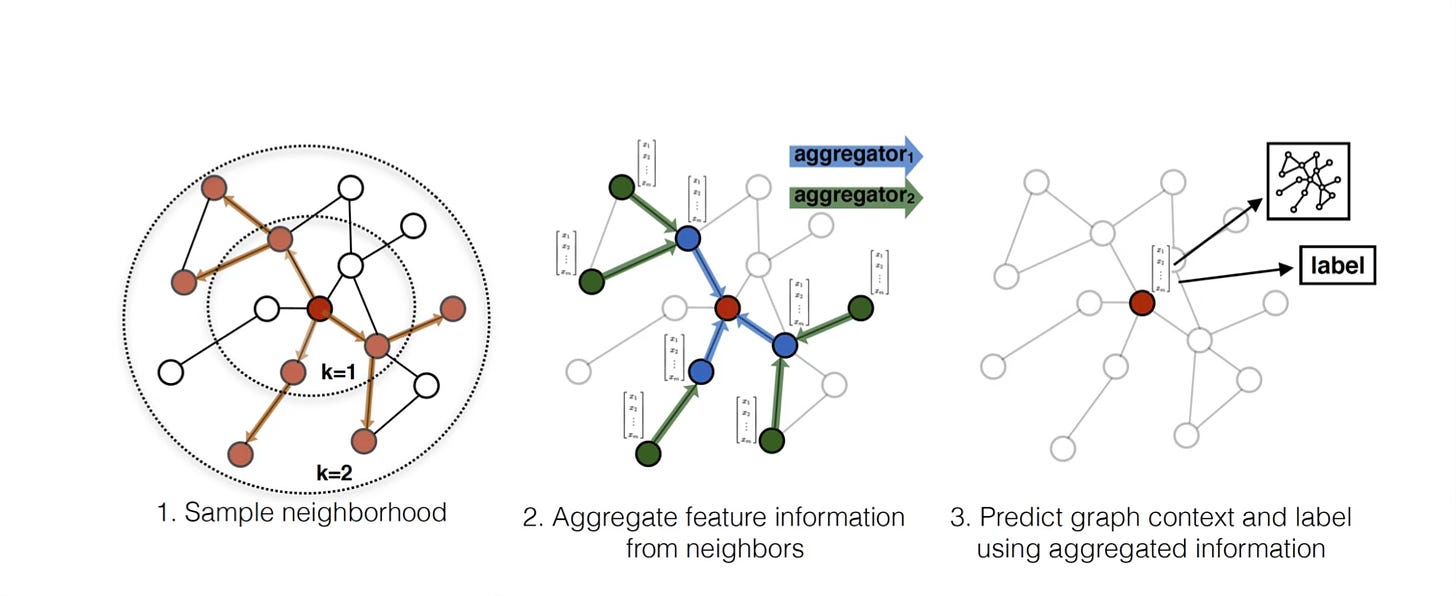
In message-passing, information is propagated between nodes of a graph along its edges. A GNN is message-passing system where each node updates its own state or embedding by gathering “messages” from its immediate neighbours. A node's understanding of the world is shaped by those directly connected to it.
Different GNN architectures differ in how nodes compose and aggregate the messages from their neighbours:
Graph Convolutional Network (GCN): Computes the element-wise mean of its neighbour's embeddings.
GraphSAGE: Computes the element-wise maximum of the embeddings of its neighbours.
Graph Attention Network (GAT): Computes a weighted sum of neighbour embeddings, where the weights are determined by an attention mechanism that considers both the current node and its neighbour.
You often require the model the interaction between two non-connected nodes i.e. non-neighbours. Message passing GNNs (MP-GNNs) achieve this by using multiple layers. While effective, this reliance on local message passing creates some fundamental challenges, especially when dealing with large, complex graphs.
Over-squashing: As information from distant nodes gets propagated through multiple layers of the GNN, it gets compressed into a fixed-size vector. This can lead to a bottleneck where important long-range dependencies are lost in the "squash."
Over-smoothing: With each message-passing step, the embeddings of nodes start to look more and more like their neighbors. After many steps, nodes in the same connected component of the graph can become indistinguishable from one another, losing their unique identities. The receptive field of a node grows exponentially with the radius of the neighbourhood.
These issues can be poetically described with a traffic analogy (due to Dominique Beaini):
Over-squashing is like being stuck in traffic - the information just can't get through efficiently.
Over-smoothing is like being lost in traffic - everything starts to look the same.
This lack of message passing propagate information effectively over the graph is also related to the expressiveness of MP-GNNs in terms of WL-test.
Graph Transformers
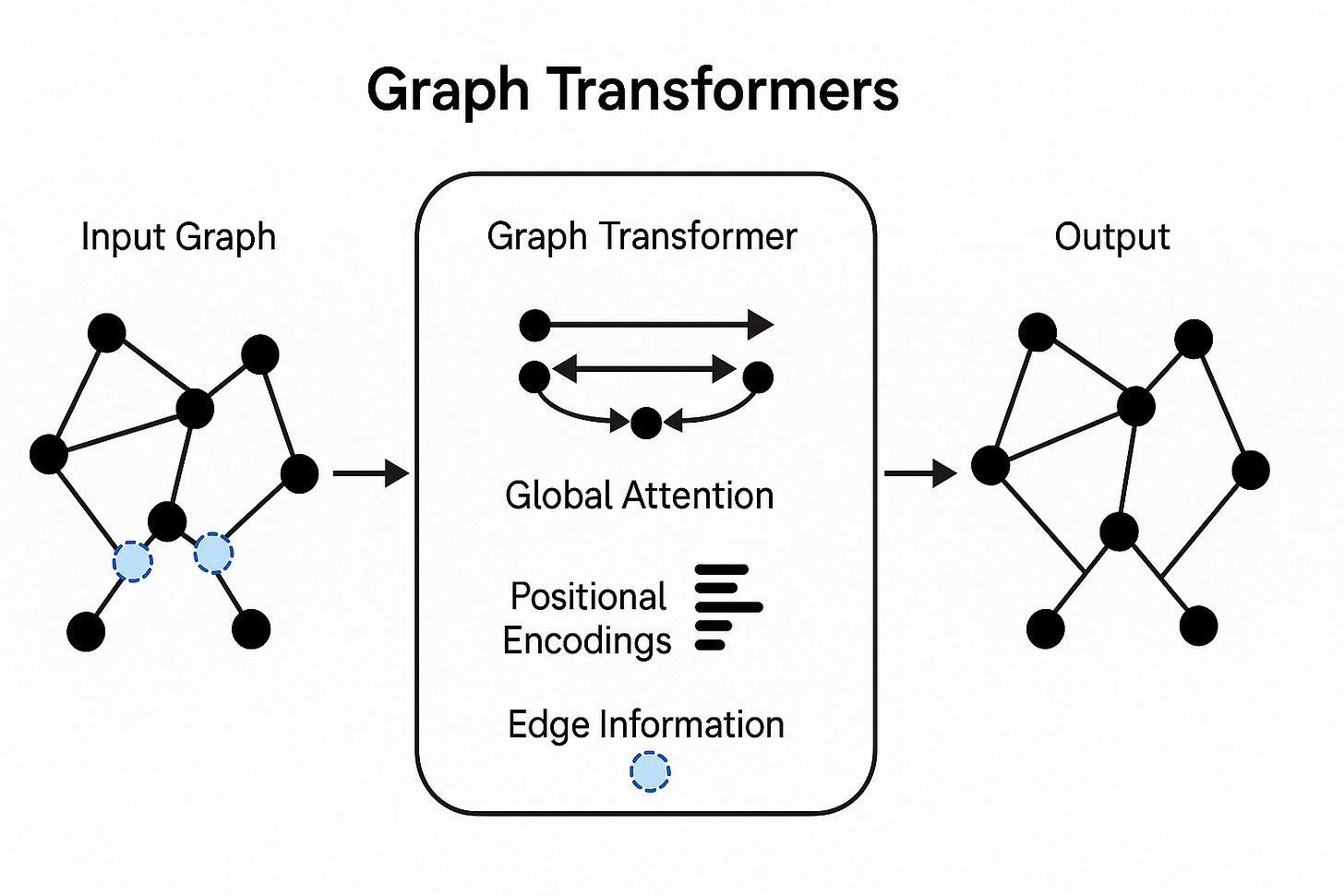
Graph transformers are an architecture proposed to alleviate the problems with MP-GNNs. Instead of passing messages between neighbours, the idea is to directly model the dependence between any two nodes in the graph. As opposed to the applying the self-attention mechanism to calculate neighbour importance as in GAT, a graph transformer applies full transformer architecture to update the embeddings of a node. This means using the standard transformer block - Multi-Head Attention + Layer Normalization + Feed-Forward Network + Residual Connections - into a graph neural network framework, making a more direct and faithful generalization of the original architecture.
The core challenge, however, is that a standard transformer is oblivious to the underlying structure of the graph. How do we inform the model about which nodes are close and which are far apart?
Ideas from NLP
Transformers by design are agnostic to underlying structure of the data and models pair-wise relations between entities. In NLP, positional encodings (PE) are used to account for the relative positions of the words in a sentence. The transformer inputs are token embedding plus positional encoding. A transformer views a sentence as a fully-connected graph of tokens, we provide structural information via PE. To be able to extend transformers to arbitrary graphs, we need a notion of positional encoding for nodes.
Graph Positional Encoding
It is challenging to design PE for graphs as there is no canonical ordering of nodes on a graph. In fact, the GNNs are designed to learn node embeddings that are independent of the node positions - this is called permutation invariance.
The choice of node PE in a graph should respect the following two constraints:
PE should be chosen such that the nearby nodes have similar PEs and the nodes that are far apart have dissimilar PEs.
The PE of a node should be unique.
Current Post
Different graph transformer architectures differ in how they leverage graph structure along with the global attention and how they design positional encodings. In the following, we will discuss different graph transformer proposals.
Laplacian Positional Encoding
The simplest possible choice for PE is to just assign an arbitrary ordering to each node. That is for each node v, PE(v) = Index(v).
However, with N nodes, there are N! possible orderings, which is computationally infeasible to learn from. In idea here is to uniformly sample an ordering from the N! possibilities such that the network is independent of the choice of the ordering.
A more powerful and theoretically grounded approach is to use the eigenvectors of the graph Laplacian as PE. The Laplacian eigenvectors form a matrix that captures the structure of the graph. They have useful properties:
Provide an embedding of the nodes into the Euclidean space.
Cognizant of the global graph structure.
Encode distance aware information i.e. nearby nodes have similar PEs, and the far apart nodes have different PEs.
The normalized Laplacian of a graph, Δ, is defined as:
where I is the identity matrix, D is the degree matrix, and A is the adjacency matrix of the graph. The Positional Encoding for a node u is then constructed using the k-smallest non-trivial eigenvectors of Δ.
The Laplacian eigenvectors can be easily computed using standard python stack.
import networkx as nx
import numpy as np
# 1. Create a sample graph: simple house-shaped graph.
G = nx.house_x_graph()
# 2. Calculate the graph Laplacian matrix
# networkx returns a SciPy sparse matrix, so we convert it to a dense numpy array.
L = nx.laplacian_matrix(G).toarray()
print("--- Graph Laplacian Matrix ---")
print(L)
# 3. Calculate eigenvalues and eigenvectors
# np.linalg.eigh is used because the Laplacian is a symmetric matrix.
# It conveniently returns eigenvalues sorted in ascending order.
eigenvalues, eigenvectors = np.linalg.eigh(L)
print("\n--- Eigenvalues ---")
print(np.round(eigenvalues, 3))
# The eigenvectors are the COLUMNS of the output matrix.
# eigenvectors[:, i] is the eigenvector for eigenvalues[i].
print("\n--- Eigenvectors (as columns) ---")
print(np.round(eigenvectors, 3))Laplacian eigenvectors can be interpreted as generalization of the sine and cosine PEs used in NLP. For a simple line graph (like a sentence), the Laplacian eigenvectors are precisely sine and cosine functions.
However, these Laplacian PEs are not perfectly unique. The eigenvectors are defined up to a sign change. To handle this ambiguity, the sign of the eigenvectors is often randomly flipped during training, making the model invariant to these sign changes.
By using the first k Laplacian eigenvectors, we drastically reduce the search space for positional information from N! possible orderings to a much smaller number of sign flips (2^k).
Laplacian Positional Encoding (LapPE) provides a principled way to encode node position that is aware of the global graph structure. It is invariant to how the nodes are ordered in the adjacency matrix. Moreover, the eigenvectors can be pre-computed, saving computational cost during training.
Graph Transformer
Now that we have a way to put positional structure on the nodes in a graph, we can build a graph transformer using the standard transformer architecture. The inputs are the direct sum of node embeddings and the node positional embedding. The attention mechanism operates locally over all the neighbouring nodes as in the message-passing GNN architectures. Now this looks quite similar to the graph attention network (GAT). In addition to using full transformer block and not just self-attention, another subtle difference is in terms of using the graph structure.
GAT: Of my direct neighbours, which one is most important for my update?
Graph Transformer: Knowing my unique structural role in the entire graph (from my PE), how should I weigh the information from my direct neighbours?
By combining the local attention mechanism of the transformer with a robust understanding of graph structure through LapPE, graph transformers are pushing the boundaries of what's possible in graph machine learning. They offer a promising path towards overcoming the limitations of traditional message-passing GNNs and unlocking new capabilities for analyzing complex, interconnected data.
Implementation
The graph transformers can be easily implemented using the PyG (torch-geometric) library. I have created a simple graph transformer model for node classification on the Cora citation network. The iPython notebook can be found on GitHub: januverma/graph-transformers. In this illustrative example, I trained a simple, smaller model which can be trained in seconds to achieve 80% accuracy. The code can be adapted for more complex problems.
Spectral Attention Networks
Laplacian Positional Encoding provides a crucial sense of node position based on the graph's structure. However, this static approach has its own set of challenges. A significant issue arises when dealing with datasets containing graphs of varying sizes, especially when there is a large disparity in the number of nodes across graphs. How do we decide on the dimension k for the positional encodings?
If we choose a small number, we risk loss of information for larger graphs.
If we choose too big, it introduces redundancy.
This creates a bottleneck and motivates a need for PE of dimension which does not depend on the number of eigenvectors in the graph. A more flexible approach is Learnable Positional Encodings (LPE).
The core idea is to use the Laplacian eigenvectors not as the final PE, but as an initialization for a learnable, end-to-end neural network module. This allows the model to learn the optimal positional representation for each node based on the entire Laplacian spectrum.
The LPE Transformer: Learning to Encode Position
Kreuzer et al. proposed a Transformer-based architecture specifically for learning these positional encodings. The LPE Transformer works as follows:
Create an Embedding Matrix: For each node
j, concatenate themsmallest eigenvaluesλwith their corresponding eigenvector valuesφat that node. This creates an initial embedding matrix of size(2,m).Linear Projection: A linear layer maps these initial embeddings to a higher
k-dimensional space.Transformer Encoder: A standard Transformer encoder processes this, applying self-attention to learn the relationships between different frequency components.
Sum Pooling: The outputs are summed along the sequence axis to produce a single, fixed-size, learned positional embedding of dimension
kfor the node.
This clever architecture learns a powerful and flexible positional encoding that is independent of the number of nodes or eigenvectors used. This network can be learned end-to-end with the whole graph transformer or can be an independently trained component. At the end, we have positional encoding for the graph.
Transformer Architecture
Once we have a robust positional encoding, we can put together a transformer architecture. The spectral attention network (SAN) uses the LPE as above and leverages full-graph attention while preserving the local connectivity of the nodes in the graph. This means that in order to calculate the next layer embedding of a node, the last layer embeddings of all the nodes in the graph are aggregated. This utilises global attention as opposed to local attention in GATs. SAN's key idea is to use two distinct attention mechanisms: one for nodes connected by actual edges and another for all other pairs of nodes, which you can think of as being connected by "virtual edges." This preserves the importance of local connectivity while enabling true, full-graph attention.
Here, r is a learnable parameter that controls the bias towards full-graph attention. SAN uses two different sets of projection matrices to compute the query, key, and value vectors - one for connected nodes and one for non-connected nodes. This allows the model to learn different types of relationships for these two scenarios.
SigNet and BasisNet
A recurring challenge with using Laplacian eigenvectors for PE is their sign ambiguity: if v is an eigenvector, then so is -v. Previously, this was handled by randomly flipping the signs during training, forcing the model to become robust to this variation. However, this is more of a workaround than a fundamental solution. This motivates the development of new architectures that are inherently sign-invariant.
SignNet offers an elegant solution to the sign ambiguity problem. The core idea is to process each eigenspace individually and then aggregate the results. To achieve sign-invariance, the network processes both v and -v separately through a shared neural network (φ), and then aggregates the results with another network (ρ).
This structure can be formally expressed as:
Where φ and ρ can be MLPs, Transformers, or other neural networks.
This design is mathematically justified. A function h is sign-invariant if and only if it can be expressed in the form h(x) = φ(x) + φ(-x) for some other function φ. Furthermore, this structure can be designed to be permutation-equivariant, meaning that if you reorder the input eigenvectors, the output is reordered in the same way. This is a crucial property for working with sets of features.
BasisNet generalizes this idea further. It can be defined as an aggregation (ρ) over a transformation (φ) applied to the outer product of each eigenvector with itself (v_i * v_i^T), which is inherently sign-invariant.
By explicitly designing architectures like SignNet and BasisNet to respect the underlying symmetries of the graph's spectral properties, we can create more robust, powerful, and theoretically sound models for graph representation learning. These networks represent the next step in the evolution of graph transformers, moving from heuristic solutions to principled designs.
The Frontier: What Lies Beyond Invariance?
The development of invariant architectures like SignNet and BasisNet solved a key theoretical problem, but the quest for better graph models is far from over. Research since has surged into new territories, focusing on scalability, architectural innovation, and even greater expressive power.
The Scalability Imperative
The biggest drawback of the vanilla transformer is its attention mechanism, which has a computational complexity of O(N^2) where N is the number of nodes. This makes it prohibitively expensive for large graphs with millions or billions of nodes. Recent work aims to break this quadratic barrier with techniques like:
Linear Attention: Using mathematical approximations (kernels) to compute attention in linear time, as seen in models like Exphormer.
Graph Sparsification: Intelligently pruning less important edges or nodes to reduce the size of the attention computation.
Hybrid Models: The "General, Powerful, and Scalable" (GPS) framework has become a popular blueprint for combining a local message-passing GNN (for efficiency) with a global attention mechanism (for expressiveness) in a modular way. Recent iterations like GPS++ further refine this recipe for state-of-the-art results.
State-Space Models and GraphMamba
Perhaps the most exciting recent development is the adaptation of State-Space Models (SSMs) as a new backbone for sequence and graph processing. Models like Mamba have challenged the dominance of the transformer in NLP by capturing long-range dependencies with linear-time complexity.
This has been adapted to graphs in models like GraphMamba. Instead of global attention, GraphMamba processes nodes as a sequence. To convert the graph into a sequence that the Mamba model can understand, it uses clever node traversal strategies, such as graph-based breadth-first or depth-first searches. By doing so, it inherits the efficiency of SSMs while effectively modeling long-range interactions along the traversal paths, offering a compelling alternative to the costly attention mechanism.
Capturing Higher-Order Structures
The next wave of innovation focuses on representing graphs at a higher level of abstraction than just nodes and edges. Research into topological deep learning and simplicial/cellular neural networks aims to capture "higher-order" structures like cycles, cliques, and cavities in a graph. These architectures promise to be more expressive by understanding the multi-level organization of complex systems, from molecular interactions to social networks.
Applications of Graph Transformers
These architectural advancements are not just theoretical; they are unlocking state-of-the-art performance in a wide range of critical domains.
Drug Discovery and Molecular Biology
Predicting the properties of a molecule (e.g., its toxicity or how well it will bind to a target protein) is a cornerstone of modern medicine. Molecules are naturally graphs, where atoms are nodes and chemical bonds are edges. A molecule's function often depends on subtle, long-range interactions between atoms that are far apart in the 2D graph structure but close in 3D space. Graph transformers' global attention can capture these crucial relationships, which local GNNs might miss, leading to more accurate predictions for drug efficacy and safety.
Physics Simulation
Simulating complex physical systems, from cosmology to fluid dynamics, involves modeling the interactions of countless particles over time. A system of particles can be seen as a graph where particles are nodes and their proximity or interaction force defines the edges. In many systems, the state of the entire system (a global property) influences individual particle interactions. GTs can model this by allowing every particle to attend to every other particle, making them highly effective for simulating complex, long-range force fields and predicting the future state of the system with greater accuracy.
Recommender Systems
Suggesting relevant items (e.g., products, movies, articles) to users from a massive catalog is a major economic problem that machine learning methods have traditionally done well at. The user-item interactions can be modeled as a large bipartite graph of users and items, with edges indicating interactions like purchases or views. Recommendations improve when you can capture higher-order relationships (e.g., "users who bought item A also bought item B, and people who like item B also tend to like item C"). Global attention allows the model to traverse these long paths of connections effortlessly, uncovering subtle trends and providing more nuanced and personalized recommendations than models that only look at a user's immediate interaction history.
Traffic and Route Prediction
The problem of forecasting traffic flow and travel times across a city's can be attempted by modeling the road network as graphs where intersections are nodes and roads are edges. Traffic is a classic example of a system with non-local effects. An accident on a major highway (one part of the graph) can cause congestion miles away on side streets (a distant part of the graph). By applying global attention, graph transformers can model these city-wide dependencies and make more accurate traffic predictions than local GNNs, which might only consider adjacent road segments.
Conclusion
The journey of graph representation learning is one of escalating ambition. We started with simple, local message-passing. To overcome its limitations, we embraced the global perspective of graph transformers, tackling the complex challenges of positional encoding and architectural symmetries. Now, the frontier has pushed even further. The latest research on scalable architectures, new backbones like State-Space Models, and higher-order topological methods is paving the way for models that are not only more powerful but also efficient enough to be deployed on the massive, web-scale graphs that define our modern world. The evolution is far from over, and the future of graph AI promises to be even more deeply connected.
References
LapPE and Graph Transformer: Dwivedi and Bresson (2021) A Generalization of Transformer Networks to Graphs, https://arxiv.org/abs/2012.09699
SAN: Kreuzer et al (2021) Rethinking Graph Transformers with Spectral Attention, https://arxiv.org/abs/2106.03893
SigNet and BasisNet: Lim at al (2022) Sign and Basis Invariant Networks for Spectral Graph Representation Learning, https://arxiv.org/abs/2202.13013
Exphormer: Shirzad et al (2023) Exphormer: Sparse Transformers for Graphs, https://arxiv.org/abs/2303.06147
GPS: Rampášek et al (2022) Recipe for a General, Powerful, Scalable Graph Transformer, https://arxiv.org/abs/2205.12454
GraphMamba: Wang el at (2024) Graph-Mamba: Towards Long-Range Graph Sequence Modeling with Selective State Spaces, https://arxiv.org/abs/2402.00789
Drug Discovery: Ying, C., et al. (2021). "Do Transformers Really Perform Badly for Graph Representation?". Advances in Neural Information Processing Systems (NeurIPS). (This paper introduced the Graphormer model and demonstrated its effectiveness on molecular property prediction benchmarks).
Physics Simulation: Li, P., et al. (2020). "Learning to Simulate Complex Physics with Graph Networks". International Conference on Machine Learning (ICML). (While using a Graph Network, this work established the paradigm of learning simulators on graphs, which later Transformer-based models built upon).
Recommender Systems: Wu, J., et al. (2020). "Graph-BERT for Recommendation". arXiv preprint arXiv:2011.09943. (This paper explores using BERT-like Transformer architectures on sampled subgraphs for recommendation tasks).
Traffic Prediction: Xu, M., et al. (2020). "Spatial-Temporal Transformer Networks for Traffic Flow Forecasting". arXiv preprint arXiv:2001.02908. (An early and influential work applying the Transformer architecture to capture both spatial and temporal dependencies in traffic networks).
If you find this post or the codes useful, I would appreciate if you can cite it as:
@misc{verma2025graph-transformers,
title={Graph Transformers: From Message Passing to Global Attention
year={2025},
url={\url{https://januverma.substack.com/p/graph-transformers}},
note={Incomplete Distillation}
}